Class 24: Spatial Data, OSMNX, GeoPandas

Class 24: Spatial Data, OSMNX, GeoPandas#

Goal of today’s class:

  1. Introduce shapefiles

  2. Introduce geopandas for spatial tasks

  3. Integrate what we learned with osmnx

  1. Come in. Sit down. Open Teams.

  2. Make sure your notebook from last class is saved.

  3. Open up the Jupyter Lab server.

  4. Open up the Jupyter Lab terminal.

  5. Activate Conda: module load anaconda3/2022.05

  6. Activate the shared virtual environment: source activate /courses/PHYS7332.202510/shared/ox/

  7. Run python3 git_fixer2.py

  8. Github:

    • git status (figure out what files have changed)

    • git add … (add the file that you changed, aka the _MODIFIED one(s))

    • git commit -m “your changes”

    • git push origin main

import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from matplotlib import rc
rc('axes', axisbelow=True)
rc('axes', fc='w')
rc('figure', fc='w')
rc('savefig', fc='w')

Introduction: Random Geometric Graphs#

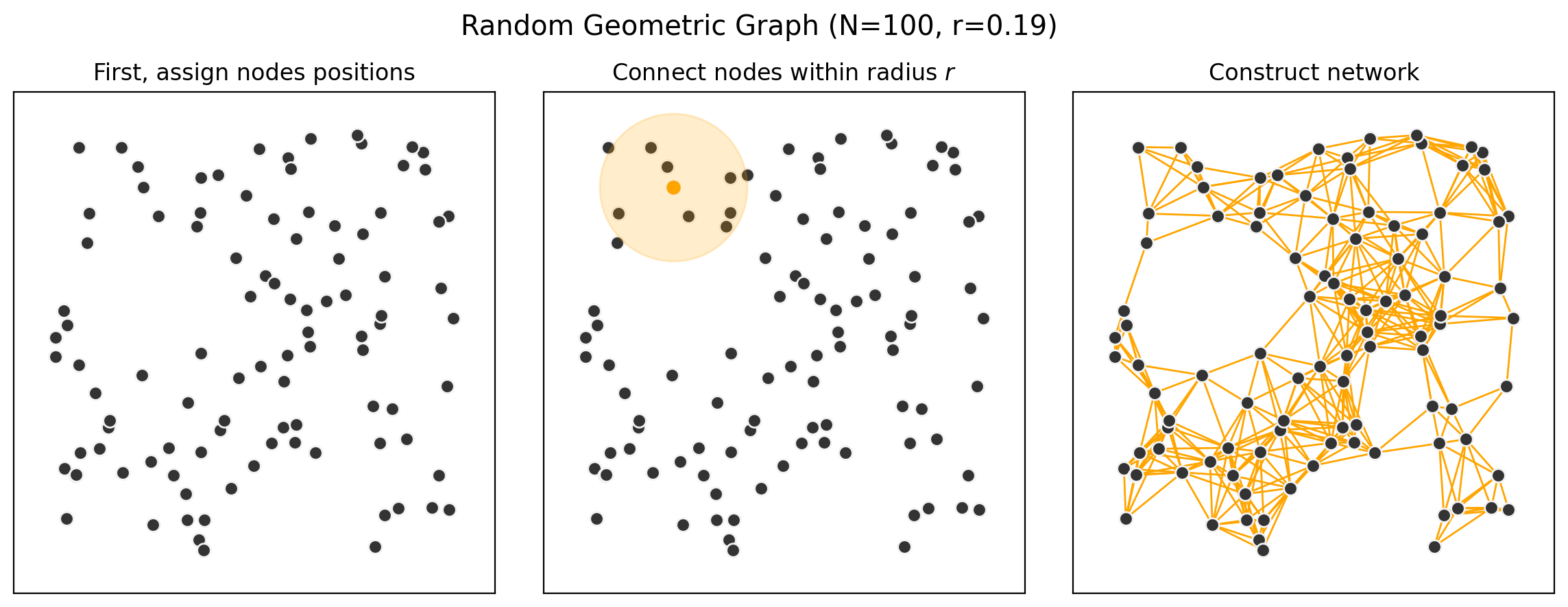
Random geometric graphs (RGGs) are spatially-embedded networks where the probability \(p_{ij}\) that any pair of nodes is connected is a function of the distance between \(i\) and \(j\). RGGs differ from classical random graphs (e.g., Erdős-Rényi graphs) by embedding nodes in space, imposing locality constraints on edge formation. This makes RGGs particularly useful for studying networks with spatial dependencies. This paradigm is useful for studying systems ranging from wireless communication networks, to transportation systems, to certain biological networks (e.g. physical connections between neurons in a brain).

A simple example of this is an RGG with \(N\) nodes, each of which are connected if they are within a given radius, \(r\), of each other. These nodes are embedded on a unit square or cube with Euclidean distance, but other spaces (e.g., toroidal, hyperbolic) can also be used.

Applications of RGGs#

  1. Wireless Networks

    • Nodes represent devices, and edges represent communication links. The radius (r) models signal range.

    • Analyze network robustness or connectivity under varying radii.

  2. Transportation Networks

    • Nodes as cities or hubs, edges based on geographic proximity.

    • Study efficient routing or identify vulnerable regions.

  3. Social Networks

    • Nodes as individuals in a physical space, edges based on interaction likelihood.

    • Explore clustering patterns in real-world social systems.

References

  1. Penrose, M. D. (2003). Random Geometric Graphs. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780198506263.001.0001

  2. Gilbert, E. N. (1961). Random plane networks. Journal of the Society for Industrial and Applied Mathematics, 9(4), 533–543. https://doi.org/10.1137/0109045

  3. Dall, J., & Christensen, M. (2002). Random geometric graphs. Physical Review E, 66(1), 016121. https://doi.org/10.1103/PhysRevE.66.016121

  4. Penrose, M. D. (1999). On \(k\)-connectivity for a geometric random graph. Random Structures & Algorithms, 15(2), 145–164. https://doi.org/10.1002/(SICI)1098-2418(199909)15:2<145::AID-RSA2>3.0.CO;2-G

  5. Barthelemy, M. (2011). Spatial networks. Physics Reports, 499(1–3), 1–101. https://doi.org/10.1016/j.physrep.2010.11.002

  6. Haenggi, M. (2009). Stochastic Geometry for Wireless Networks. Cambridge University Press. https://doi.org/10.1017/CBO9781139043816

  7. Eppstein, D., Goodrich, M. T., & Trott, L. (2009, November). Going off-road: transversal complexity in road networks. In Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems (pp. 23-32). https://doi.org/10.1145/1653771.1653778

Creating an RGG in Python#

np.random.seed(5)
N = 100
r = 0.19 # Connection radius

# Randomly place nodes in a unit square
positions = np.random.rand(N, 2)

# Create the graph
G = nx.Graph()
G.add_nodes_from(list(range(N)))
pos = dict(zip(G.nodes(),positions))

# Add edges based on Euclidean distance
for i in range(N):
    for j in range(i + 1, N):
        distance = np.linalg.norm(positions[i] - positions[j])
        if distance <= r:
            G.add_edge(i, j)

fig, ax = plt.subplots(1,3,figsize=(14.5,4.75),dpi=200,sharex=True,sharey=True)
plt.subplots_adjust(wspace=0.1)

# First
nx.draw_networkx_nodes(G, pos, node_size=50, ax=ax[0], node_color='.2', edgecolors='.95')

# Second
nx.draw_networkx_nodes(G, pos, node_size=50, ax=ax[1], node_color='.2', edgecolors='.95')
ax[1].scatter(positions[:,0][:1],positions[:,1][:1], s=40, color='orange', zorder=201)
ax[1].scatter(positions[:,0][:1],positions[:,1][:1], alpha=0.2, s=6000, color='orange', zorder=200)

# Third
nx.draw_networkx_nodes(G, pos, node_size=50, ax=ax[2], node_color='.2', edgecolors='.95')
nx.draw_networkx_edges(G, pos, edge_color='orange', ax=ax[2])

ax[0].set_title('First, assign nodes positions')
ax[1].set_title('Connect nodes within radius $r$')
ax[2].set_title('Construct network')


plt.suptitle("Random Geometric Graph (N=%i, r=%.2f)"%(N,r),fontsize='x-large',y=1)


plt.show()
_images/111b1591c5396627324737cab1117a877f08e49f22b108d3e06dea5b36d8e936.png

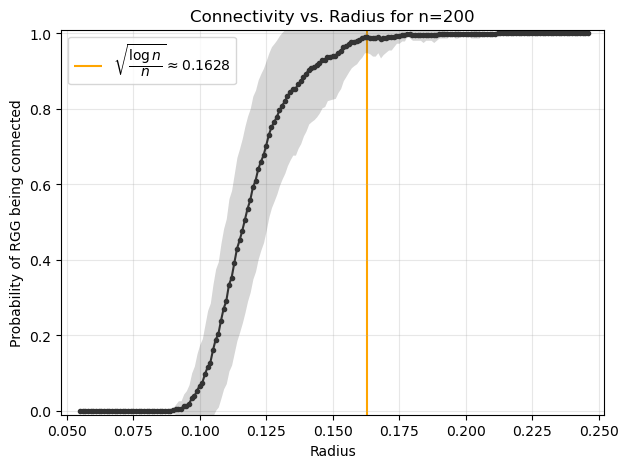
Key Properties of RGGs#

  1. An important question in RGGs is the relationship between the connectivity radius \(r\) and the number of nodes \(n\). For a graph to be fully connected: \( r \propto \sqrt{\frac{\log n}{n}} \). This ensures that, as \(n\) increases, the probability of the graph being connected approaches 1.

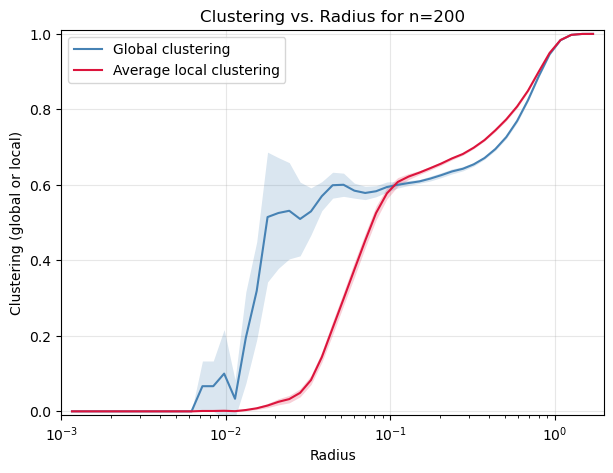
  2. The clustering coefficient of an RGG tends to be high because nodes are connected based on spatial proximity, leading to local clusters. This is a distinguishing feature compared to random graphs like Erdős–Rényi graphs, where clustering is typically lower.

  3. The degree of a node in an RGG is determined by the number of nodes within the radius \(r\), which is proportional to the area of the neighborhood: \(\langle k \rangle = n \pi r^2 \). For larger \(n\), the degree distribution tends to follow a binomial distribution, approximated by a normal distribution.

niter = 100
n = 200
radii = np.linspace(0.05, 0.25, 201).round(5)

connected_mean = []
connected_stdv = []
for ri,r in enumerate(radii):
    if ri%10==0:
        print(np.round(r,5))
    tmp = []
    for _ in range(niter):
        G = nx.random_geometric_graph(n, r)
        tmp.append(nx.is_connected(G))

    connected_mean.append(np.mean(tmp))
    connected_stdv.append(np.std(tmp))


# convert to 
connected_mean = np.array(pd.Series(connected_mean).rolling(window=10,center=True).mean())
connected_stdv = np.array(pd.Series(connected_stdv).rolling(window=10,center=True).mean())

0.05

0.06

0.07

0.08

0.09

0.1

0.11

0.12

0.13

0.14

0.15

0.16

0.17

0.18

0.19

0.2

---------------------------------------------------------------------------
KeyboardInterrupt                         Traceback (most recent call last)
Cell In[6], line 12
     10 tmp = []
     11 for _ in range(niter):
---> 12     G = nx.random_geometric_graph(n, r)
     13     tmp.append(nx.is_connected(G))
     15 connected_mean.append(np.mean(tmp))

File <class 'networkx.utils.decorators.argmap'> compilation 5:4, in argmap_random_geometric_graph_1(n, radius, dim, pos, p, seed, pos_name, backend, **backend_kwargs)
      2 import collections
      3 import gzip
----> 4 import inspect
      5 import itertools
      6 import re

File /opt/hostedtoolcache/Python/3.11.10/x64/lib/python3.11/site-packages/networkx/utils/backends.py:967, in _dispatchable.__call__(self, backend, *args, **kwargs)
    965     if backend is not None and backend != "networkx":
    966         raise ImportError(f"'{backend}' backend is not installed")
--> 967     return self.orig_func(*args, **kwargs)
    969 # Use `backend_name` in this function instead of `backend`.
    970 # This is purely for aesthetics and to make it easier to search for this
    971 # variable since "backend" is used in many comments and log/error messages.
    972 backend_name = backend

File /opt/hostedtoolcache/Python/3.11.10/x64/lib/python3.11/site-packages/networkx/generators/geometric.py:204, in random_geometric_graph(n, radius, dim, pos, p, seed, pos_name)
    201     pos = {v: [seed.random() for i in range(dim)] for v in G}
    202 nx.set_node_attributes(G, pos, pos_name)
--> 204 G.add_edges_from(_geometric_edges(G, radius, p, pos_name))
    205 return G

File /opt/hostedtoolcache/Python/3.11.10/x64/lib/python3.11/site-packages/networkx/classes/graph.py:1049, in Graph.add_edges_from(self, ebunch_to_add, **attr)
   1047     self._adj[v] = self.adjlist_inner_dict_factory()
   1048     self._node[v] = self.node_attr_dict_factory()
-> 1049 datadict = self._adj[u].get(v, self.edge_attr_dict_factory())
   1050 datadict.update(attr)
   1051 datadict.update(dd)

KeyboardInterrupt: 

fig, ax = plt.subplots(1,1,figsize=(7,5),dpi=100)


ax.plot(radii, connected_mean, marker=".", color='.2')
ax.fill_between(radii,
                connected_mean-connected_stdv/2,
                connected_mean+connected_stdv/2,
                alpha=0.2, lw=0, color='.2')

ax.vlines(np.sqrt(np.log(n)/n),-1,2, color='orange', zorder=0,
          label=r'$\sqrt{\dfrac{\log n}{n}} \approx %.4f$'%(np.sqrt(np.log(n)/n)))

ax.legend()

ax.set_xlabel("Radius")
ax.set_ylabel("Probability of RGG being connected")
ax.set_title(f"Connectivity vs. Radius for n={n}")

ax.grid(alpha=0.3)
ax.set_ylim(-0.01,1.01)
ax.set_xlim(min(radii)-0.002,max(radii)+0.002)


plt.show()
_images/4d8d48c962d2f0e048bfe5017dee990b35b209baefb12f506f9cb712e4f91517.png

Your turn!#

Repeatedly generate RGGs with \(n=300\), and analyze how the average clustering coefficient changes with radius \(r\). Create a plot of clustering coefficient vs. radius.

niter = 10
n = 200
radii = np.logspace(-3, 0.3, 51).round(5)

triangles_mean = []
triangles_stdv = []
cc_mean = []
cc_stdv = []
for ri,r in enumerate(radii):
    if ri%10==0:
        print(np.round(r,5))
    tmp = []
    tmp_cc = []
    for _ in range(niter):
        G = nx.random_geometric_graph(n, r)
        tt = nx.transitivity(G)
        tt = tt if not np.isnan(tt) else 1.0
        tmp.append(tt)
        tmp_cc.append(nx.average_clustering(G))

    triangles_mean.append(np.nanmean(tmp))
    triangles_stdv.append(np.nanstd(tmp))
    cc_mean.append(np.nanmean(tmp_cc))
    cc_stdv.append(np.nanstd(tmp_cc))


# convert to 
triangles_mean = np.array(pd.Series(triangles_mean).rolling(window=3,center=True).mean())
triangles_stdv = np.array(pd.Series(triangles_stdv).rolling(window=3,center=True).mean())

cc_mean = np.array(pd.Series(cc_mean).rolling(window=3,center=True).mean())
cc_stdv = np.array(pd.Series(cc_stdv).rolling(window=3,center=True).mean())

0.001
0.00457
0.02089
0.0955
0.43652
1.99526

fig, ax = plt.subplots(1,1,figsize=(7,5),dpi=100)


ax.semilogx(radii, triangles_mean, color='steelblue', label='Global clustering')
ax.fill_between(radii,
                triangles_mean-triangles_stdv/2,
                triangles_mean+triangles_stdv/2,
                alpha=0.2, lw=0, color='steelblue')

ax.semilogx(radii, cc_mean, color='crimson', label='Average local clustering')
ax.fill_between(radii,
                cc_mean-cc_stdv/2,
                cc_mean+cc_stdv/2,
                alpha=0.2, lw=0, color='crimson')


ax.legend()

ax.set_xlabel("Radius")
ax.set_ylabel("Clustering (global or local)")
ax.set_title(f"Clustering vs. Radius for n={n}")

ax.grid(alpha=0.3)
ax.set_ylim(-0.01,1.01)
ax.set_xlim(min(radii),max(radii))


plt.show()
_images/824c3ebc74a6cdd982097f5ff66cdfd1f112612ec1cc07c283cd501f2221a574.png

Open Street Maps NetworkX, aka OSMnx#

From the readthedocs: “OSMnx is a Python package to easily download, model, analyze, and visualize street networks and other geospatial features from OpenStreetMap. You can download and model walking, driving, or biking networks with a single line of code then analyze and visualize them. You can just as easily work with urban amenities/points of interest, building footprints, transit stops, elevation data, street orientations, speed/travel time, and routing.”

Key features of OSMnx#

  1. Network Retrieval: Automatically download and construct spatial networks from OpenStreetMap, specifying geographic boundaries (e.g., a city, region, or bounding box) or by name.

  2. Customizability: Filter networks by type (e.g., walkable, drivable, bikeable), attributes (e.g., one-way streets, speed limits), or custom tags from OpenStreetMap.

  3. Graph Representation: Represent spatial data as directed or undirected graphs, complete with geometric edge and node attributes for spatial analysis.

  4. Visualization: Create static or interactive visualizations of networks with minimal effort, utilizing underlying geometric and topological properties.

  5. Integration with GIS: Export networks and spatial data to standard GIS formats, such as Shapefiles and GeoPackages, for integration into broader geospatial workflows.

References:

  1. Boeing, G. (2024). Modeling and Analyzing Urban Networks and Amenities with OSMnx. Working paper. https://geoffboeing.com/publications/osmnx-paper/

  2. Boeing, G. (2017). OSMnx: New methods for acquiring, constructing, analyzing, and visualizing complex street networks. Computers, Environment and Urban Systems, 65, 126–139. https://doi.org/10.1016/j.compenvurbsys.2017.05.004.

  3. Boeing, G. (2022). Street network models and indicators for every urban area in the world. Geographical Analysis, 54(3), 519-535. https://doi.org/10.1111/gean.12281.

Examples#

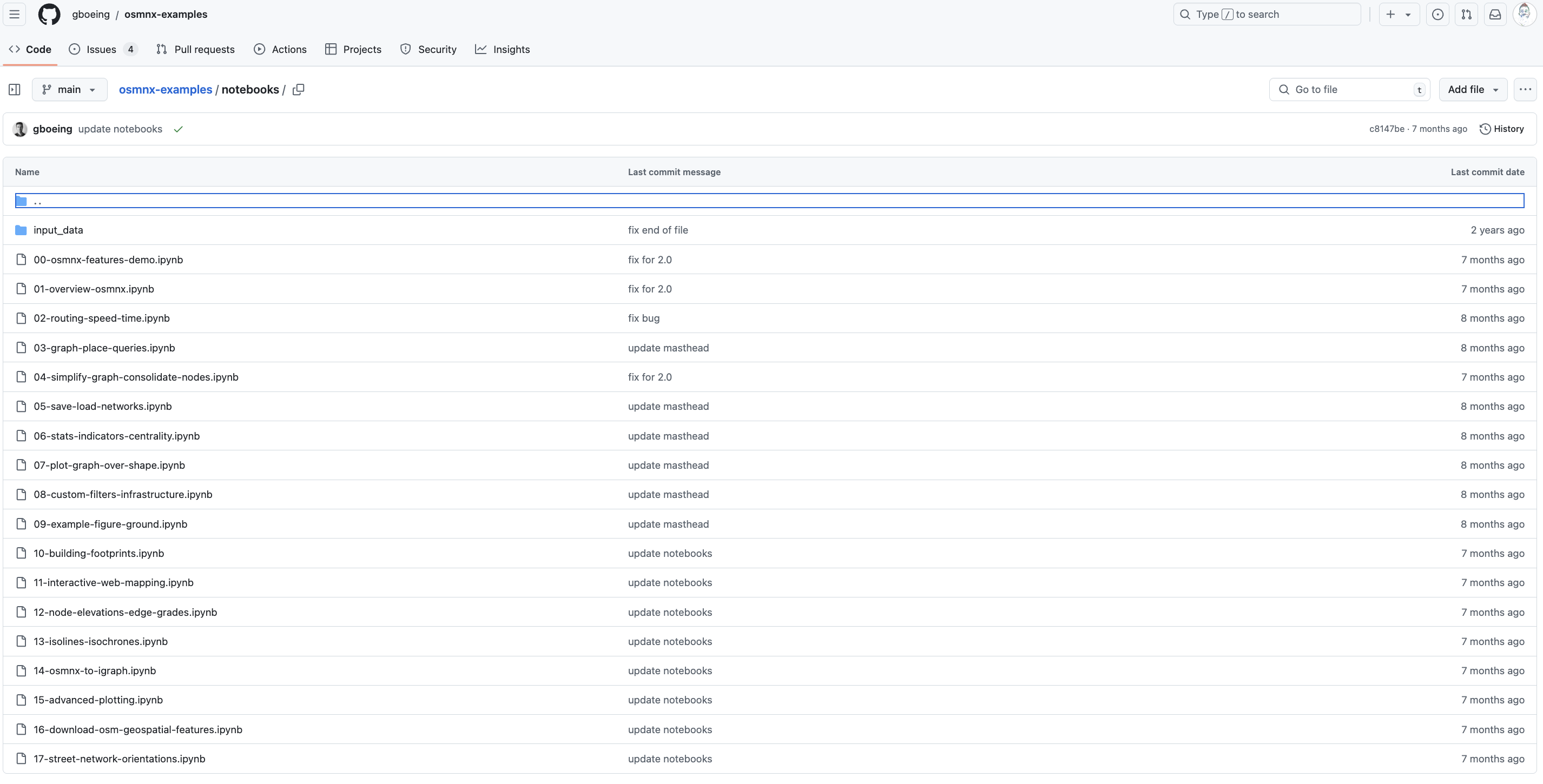
Our first exploration comes from the terrific Examples Gallery of osmnx

gboeing/osmnx-examples

import osmnx as ox
ox.__version__

'2.0.0'

G = ox.graph_from_place("Boston, Massachusetts, USA", network_type="drive")

G.number_of_nodes(), G.number_of_edges()

(11138, 25495)

list(G.nodes(data=True))[:2]

[(30730954, {'y': 42.3676084, 'x': -71.0218168, 'street_count': 3}),
 (61178875, {'y': 42.3821495, 'x': -71.0808776, 'street_count': 4})]

list(G.edges(data=True))[:2]

[(30730954,
  61441677,
  {'osmid': 197230699,
   'highway': 'residential',
   'lanes': '2',
   'maxspeed': '25 mph',
   'name': 'Logan Memorial Way',
   'oneway': True,
   'reversed': False,
   'length': np.float64(33.07297223949995),
   'geometry': <LINESTRING (-71.022 42.368, -71.022 42.368, -71.022 42.368, -71.022 42.368)>}),
 (30730954,
  1102741801,
  {'osmid': 197230701,
   'highway': 'residential',
   'maxspeed': '25 mph',
   'name': 'Logan Memorial Way',
   'oneway': False,
   'reversed': False,
   'length': np.float64(278.88651649604105),
   'geometry': <LINESTRING (-71.022 42.368, -71.022 42.368, -71.022 42.368, -71.022 42.367,...>})]

fig, ax = plt.subplots(1,1,figsize=(4,4),dpi=200)
ox.plot_graph(G, ax=ax, bgcolor='white', node_color='steelblue', node_size=2, edge_linewidth=0.1)

plt.show()
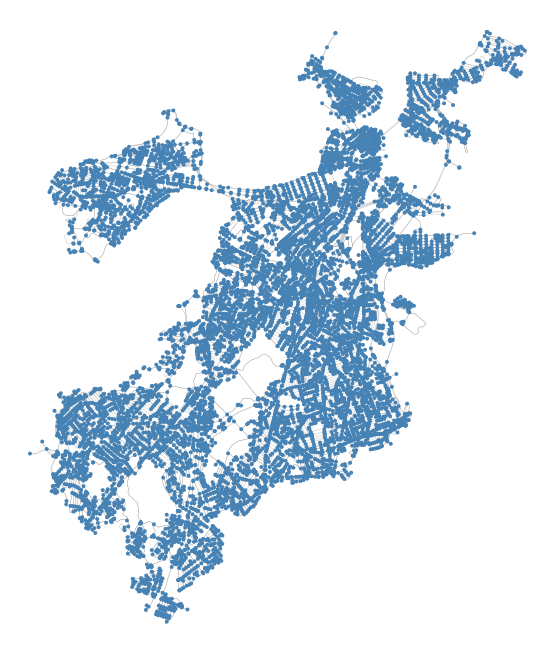
_images/7fffe10e2d8d7ae62f9eb8646b9a3a941d5c0976a1644af2261baeb8d1ca72fa.png

From the OSMnx Features Demo notebook:

OSMnx geocodes the query “Boston, Massachusetts, USA” to retrieve the place boundaries of that city from the Nominatim API, retrieves the drivable street network data within those boundaries from the Overpass API, constructs a graph model, then simplifies/corrects its topology such that nodes represent intersections and dead-ends and edges represent the street segments linking them. All of this is discussed in detail in the documentation and these examples. OSMnx models all networks as NetworkX MultiDiGraph objects. You can convert to:

  • undirected MultiGraphs

  • DiGraphs without (possible) parallel edges

  • GeoPandas node/edge GeoDataFrames

G = ox.graph_from_place("Roslindale, Massachusetts, USA", network_type="drive")

xpos = nx.get_node_attributes(G,'x')
ypos = nx.get_node_attributes(G,'y')
pos_init = {i:(xpos[i],ypos[i]) for i in G.nodes()}

np.random.seed(5)
pos_network = nx.spring_layout(G, pos=pos_init, k=0.001, iterations=200)

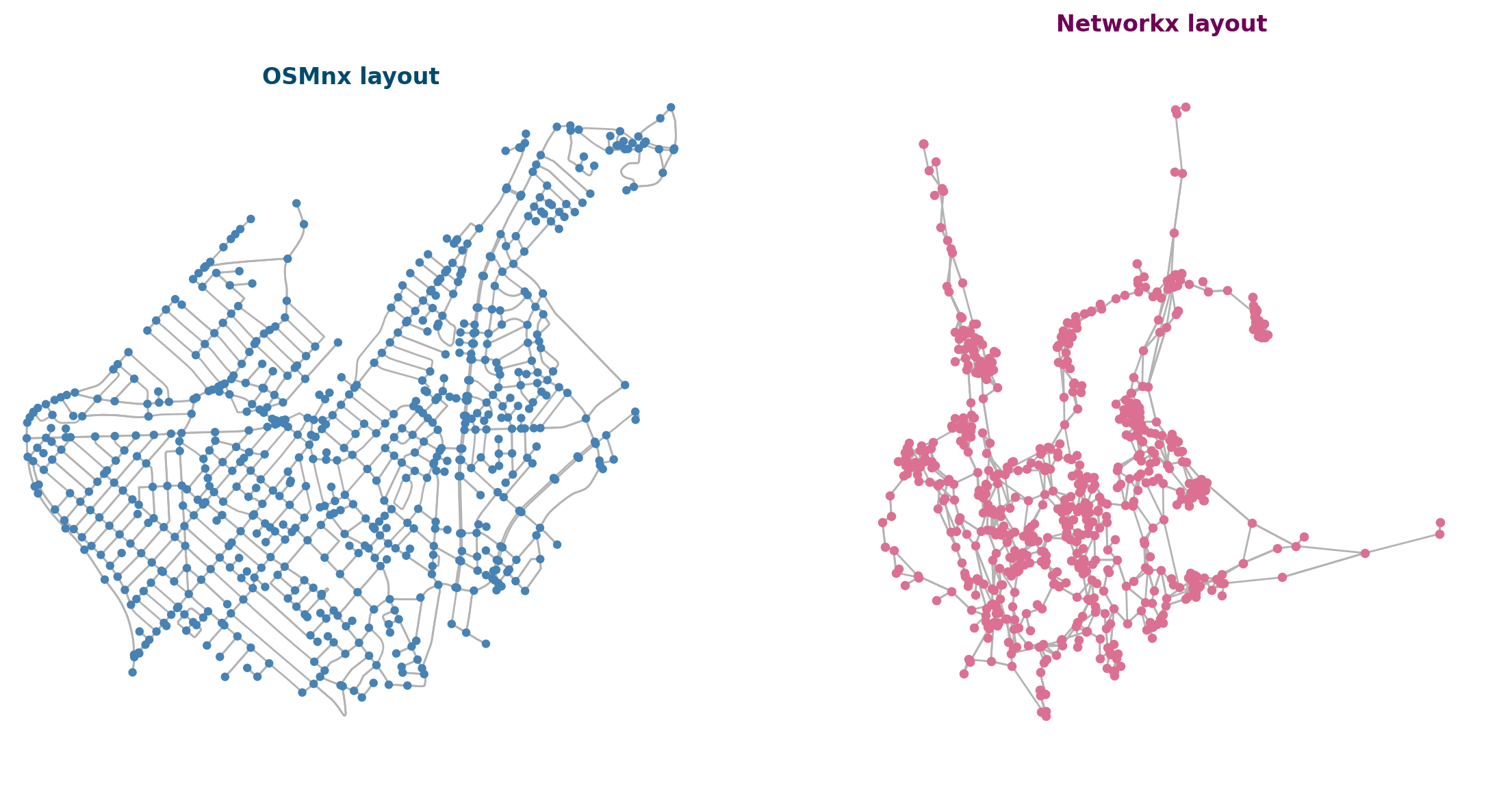
fig, ax = plt.subplots(1,2,figsize=(14,7),dpi=200)

nx.draw_networkx_nodes(G, pos=pos_network, node_size=15, node_color='palevioletred', ax=ax[1])
nx.draw_networkx_edges(G, pos=pos_network, edge_color='.7', width=1.0, arrows=False, ax=ax[1])
ax[1].set_axis_off()

ax[0].set_title('OSMnx layout',fontweight='bold',color='#004a6f')
ax[1].set_title('Networkx layout',fontweight='bold',color='#6f0056')

ox.plot_graph(G, ax=ax[0], bgcolor='white', node_color='steelblue', edge_color='.7', node_size=20)


plt.show()
_images/7662cd14cf23da52fbac3dc2d1631840ac5251a495f92a8a41746ffa6b26c1e6.png 
tags = {"building": True}
gdf = ox.features_from_place("Roslindale, Massachusetts, USA", tags)

gdf_proj = ox.projection.project_gdf(gdf)

bldg_colors = dict(zip(gdf_proj['building'].unique(),
                       plt.cm.tab20c(np.linspace(0,1,gdf_proj['building'].nunique()))))
bcs = [bldg_colors[i] for i in gdf_proj['building'].values]

fig, ax = ox.plot_footprints(gdf_proj, bgcolor='.1',
                             color=bcs, dpi=400, show=False, close=False)
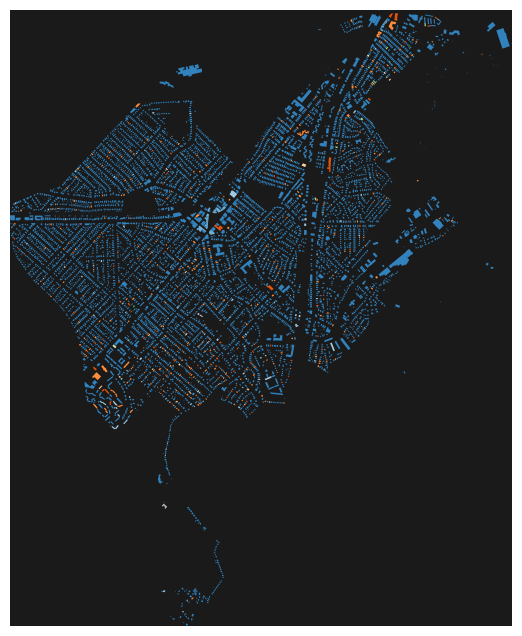
_images/d4a0db9252450ccfecf6646061c81c338f4a8a3d8023abc30855b9292be14c76.png 
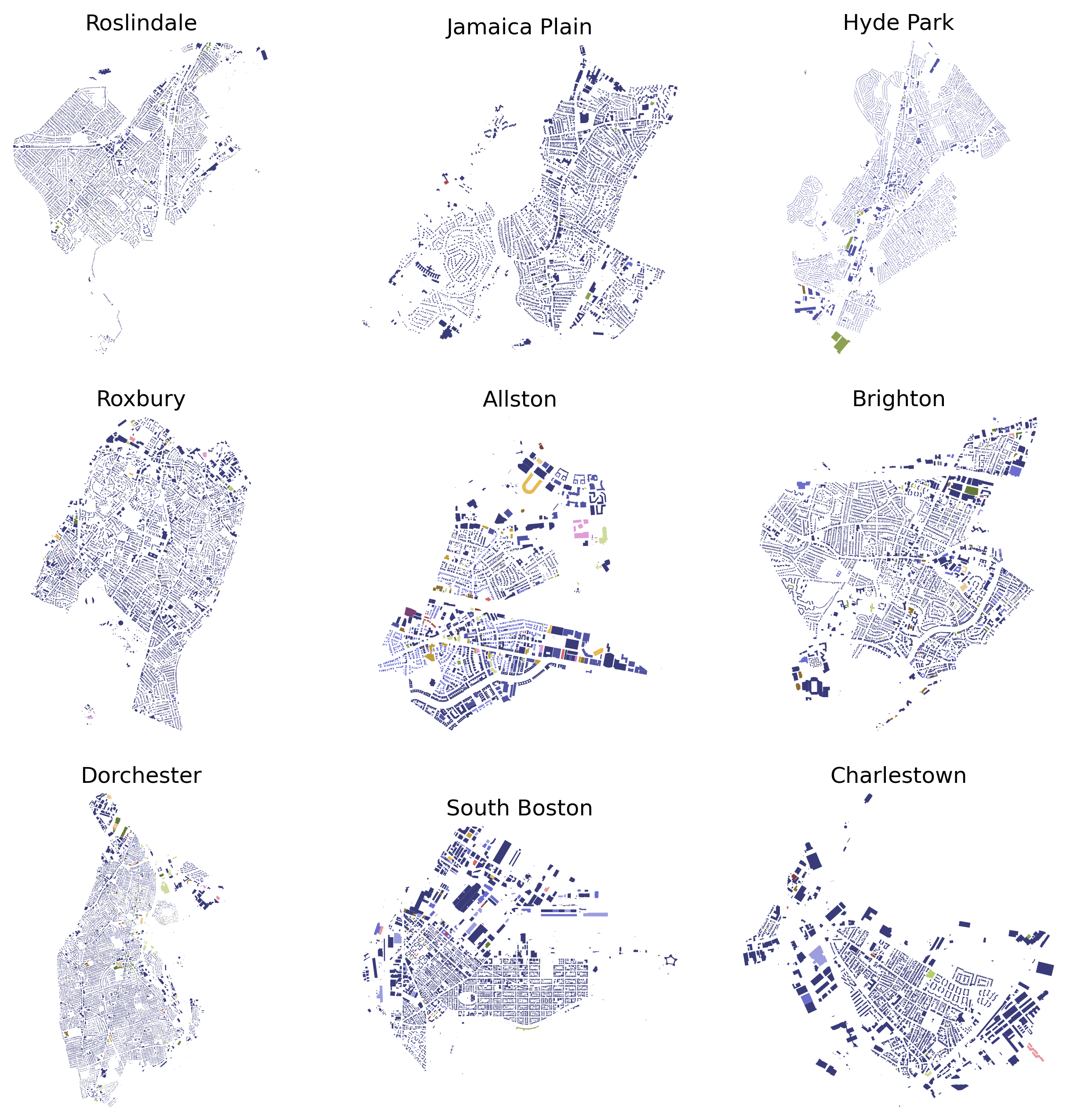
import itertools as it
ncols = 3
nrows = 3
tups = list(it.product(range(nrows), range(ncols)))

fig, ax = plt.subplots(nrows,ncols,figsize=(ncols*3.5,nrows*3.5),dpi=300)

neighborhoods = ["Roslindale, Massachusetts, USA", 
                 "Jamaica Plain, Massachusetts, USA",
                 "Hyde Park, Massachusetts, USA",
                 "Roxbury, Massachusetts, USA",
                 "Allston, Massachusetts, USA",
                 "Brighton, Massachusetts, USA",
                 "Dorchester, Massachusetts, USA",
                 "South Boston, Massachusetts, USA",
                 "Charlestown, Massachusetts, USA"]

for ix, neigh in enumerate(neighborhoods):
    print(neigh)
    gdf = ox.features_from_place(neigh, tags)
    gdf_proj = ox.projection.project_gdf(gdf)
    bldg_colors = dict(zip(gdf_proj['building'].unique(),
                           plt.cm.tab20b(np.linspace(0,1,gdf_proj['building'].nunique()))))
    bcs = [bldg_colors[i] for i in gdf_proj['building'].values]    
    ox.plot_footprints(gdf_proj, bgcolor='.1', ax=ax[tups[ix]],
                       color=bcs, dpi=400, show=False, close=False)
    ax[tups[ix]].set_title(neigh.split(',')[0])

plt.show()

Roslindale, Massachusetts, USA
Jamaica Plain, Massachusetts, USA
Hyde Park, Massachusetts, USA
Roxbury, Massachusetts, USA
Allston, Massachusetts, USA
Brighton, Massachusetts, USA
Dorchester, Massachusetts, USA
South Boston, Massachusetts, USA
Charlestown, Massachusetts, USA
_images/439e829113209924716b00ae1c4ca692bfc736c22d1c38cbc10d4357c63bd618.png

A little fun#

bk_home = (42.28615490099605, -71.12870104902592)
one_mile = 1609  # meters
two_mile = one_mile*2  # meters
five_mile = one_mile*5  # meters
dist = one_mile
# dist = two_mile
# dist = five_mile
G = ox.graph_from_point(bk_home, dist=dist, network_type="walk")

# convert your MultiDiGraph to an undirected MultiGraph
M = ox.convert.to_undirected(G)

# convert your MultiDiGraph to a DiGraph without parallel edges
D = ox.convert.to_digraph(G)

# api_key = ''
G = ox.elevation.add_node_elevations_google(G, api_key=api_key)
G = ox.elevation.add_edge_grades(G)

ehs1 = np.array(list(nx.edge_betweenness_centrality(G).values()))
mehs1 = (max(ehs1)-ehs1) / (max(ehs1)-min(ehs1))
ecs1 = plt.cm.magma(mehs1**50*0.9)

ehs2 = np.array(list(nx.get_edge_attributes(G, 'grade').values()))
mehs2 = (max(ehs2)-ehs2) / (max(ehs2)-min(ehs2))
ecs2 = plt.cm.Spectral_r(mehs2**2)

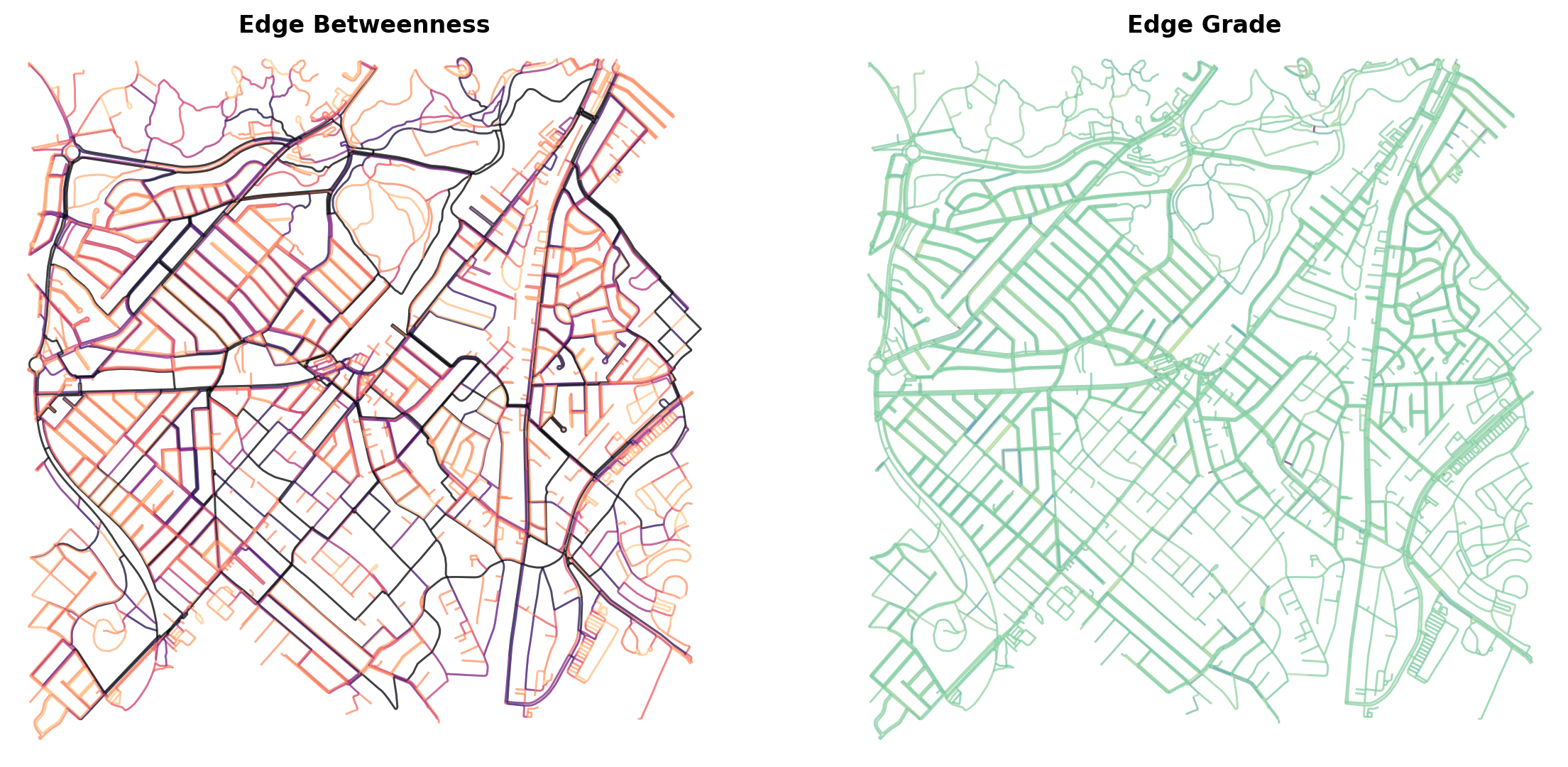
fig, ax = plt.subplots(1,2,figsize=(14,7),dpi=200)

ox.plot_graph(G, node_size=0, bgcolor='white', edge_linewidth=1.0,
              edge_color=ecs1, edge_alpha=0.5, ax=ax[0], show=False, close=False)

ox.plot_graph(G, node_size=0, bgcolor='white', edge_linewidth=1.0,
              edge_color=ecs2, edge_alpha=0.5, ax=ax[1], show=False, close=False)


ax[0].set_title('Edge Betweenness',fontweight='bold')
ax[1].set_title('Edge Grade',fontweight='bold')


plt.show()
_images/5c8e2dce57b1e8ccb8a2c136f0b1400c472dc60f9345d86269348dc7b56c4467.png

Your turn! (15 minutes)#

With a partner:

  1. Find the latitute and longitude of where you’re from (could be birthplace, where you call home, where you grew up, etc.)

  2. Use osmnx to collect the street network within a 2 mile radius of your home coordinates

  3. Find a way to quantify the dissimilarities between these two networks

  4. Compare these street networks to Erdős-Rényi graphs with the same size/density

pass

Geopandas#

GeoPandas is a Python library that extends the functionality of Pandas to support geospatial data. It provides tools for working with vector data, enabling the analysis and visualization of spatial datasets such as points, lines, and polygons. Built on top of Pandas and shapely, and integrating seamlessly with Fiona and pyproj, GeoPandas simplifies handling geospatial data, making it accessible to data scientists and analysts without the need for specialized GIS software.

Geopandas handles spatial data types, known as Points, LineStrings, and Polygons using shapely geometries. It enables us to do a range of spatial analyses, such as buffering, intersection, union, spatial joins, and clipping. It supports reading from and writing to common geospatial file formats, such as Shapefiles, GeoJSON, and GeoPackage.

References

  1. Jordahl, K. (2014). GeoPandas: Python tools for geographic data. https://geopandas.org

Shapefiles#

GeoPandas is built to work seamlessly with geospatial data in various formats, with Shapefiles being one of the most widely used. Shapefiles are a geospatial vector data format developed by ESRI, widely used for representing geographic features like points, lines, and polygons. Despite their ubiquity, Shapefiles have some limitations that users should understand when working with GeoPandas.

Key Components of a Shapefile#

A Shapefile is actually a collection of at least three mandatory files:

  1. .shp: Stores geometry data (e.g., points, line segments, or polygons).

  2. .shx: Index file for quick access to the geometry data in the .shp.

  3. .dbf: Stores attribute data (e.g., names, IDs, or other metadata) in tabular form.

Optional files include:

  • .prj: Specifies the projection and coordinate reference system (CRS).

  • .cpg: Stores character encoding information.

  • .xml: Metadata about the Shapefile.

Terrific resource can be found here!

Other Geospatial File Formats Supported by GeoPandas#

GeoPandas supports a variety of more modern and flexible file formats:

GeoJSON#

  • Description: A lightweight, JSON-based format for encoding a variety of geographic data structures.

  • Strengths:

    • Human-readable and easy to parse.

    • Ideal for web applications due to its JSON format.

    • Supports multiple geometry types in a single file.

  • Limitations:

    • Limited support for very large datasets.

    • Less efficient for heavy computations compared to binary formats.

GeoPackage#

  • Description: A modern, SQLite-based container format for vector and raster data.

  • Strengths:

    • Single-file format, unlike Shapefiles.

    • Supports large datasets and complex attribute data.

    • Handles projections and CRS more robustly.

  • Limitations:

    • Larger file size compared to some lightweight formats.

    • Newer standard, so not universally supported by older software.

GeoPandas I/O Capabilities#

GeoPandas uses Fiona under the hood for geospatial file I/O, enabling support for these formats. Key functions include:

  1. Reading Geospatial Files:

    import geopandas as gpd
gdf = gpd.read_file("path/to/file.shp")

  2. Writing Geospatial Files:

    gdf.to_file("path/to/output.geojson", driver="GeoJSON")

  3. Handling CRS: GeoPandas automatically reads CRS metadata when present:

    gdf.crs  # Access CRS
gdf = gdf.to_crs("EPSG:4326")  # Reproject to a new CRS

import geopandas as gpd

ma = gpd.read_file('data/tl_2020_25_tract')

ma.head()
STATEFP COUNTYFP TRACTCE GEOID NAME NAMELSAD MTFCC FUNCSTAT ALAND AWATER INTPTLAT INTPTLON geometry
0 25 009 265102 25009265102 2651.02 Census Tract 2651.02 G5020 S 16318373 134252 +42.7338220 -070.9600766 POLYGON ((-70.99091 42.73399, -70.99089 42.734...
1 25 009 268200 25009268200 2682 Census Tract 2682 G5020 S 10737361 364499 +42.8117773 -070.9054643 POLYGON ((-70.92052 42.79103, -70.9205 42.7910...
2 25 009 268400 25009268400 2684 Census Tract 2684 G5020 S 3065747 4715475 +42.8054407 -070.8329685 POLYGON ((-70.87547 42.79793, -70.87547 42.797...
3 25 009 250500 25009250500 2505 Census Tract 2505 G5020 S 300558 3894 +42.7169313 -071.1693673 POLYGON ((-71.17166 42.72127, -71.1709 42.7208...
4 25 027 731300 25027731300 7313 Census Tract 7313 G5020 S 743090 7345 +42.2513743 -071.8152408 POLYGON ((-71.82361 42.24948, -71.8228 42.2499...

What do we notice here?

ma.plot()

<Axes: >
_images/111d81acb731ec29e847bd6d9e8cff0c0db4187d7c58f8d43d174f684a0ebedb.png 
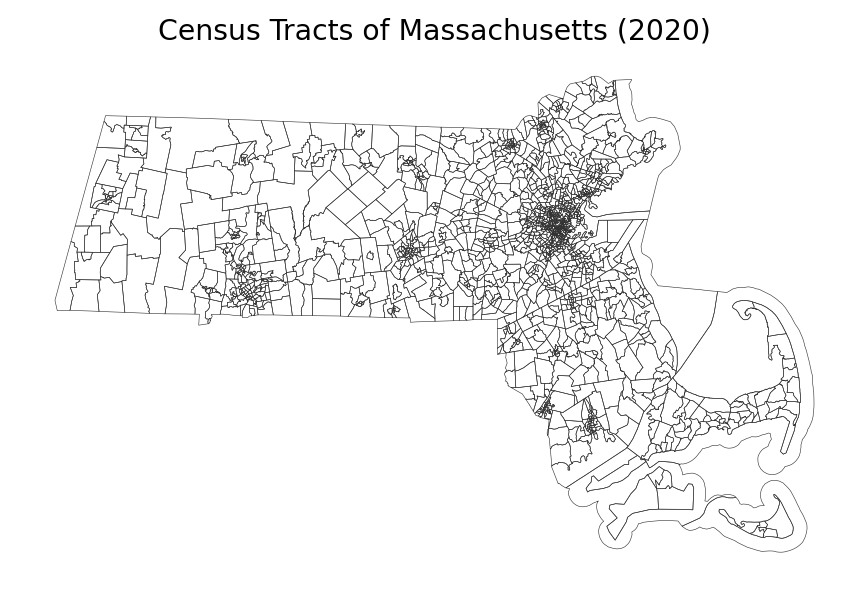
fig, ax = plt.subplots(1, 1, figsize=(8, 4), dpi=170)

ma.plot(fc='none', ec='.2', lw=0.25, ax=ax)
ax.set_title('Census Tracts of Massachusetts (2020)')
ax.set_axis_off()

plt.show()
_images/80775bfcac2ffe4d0cbe69fa7b1665e27a72b29552189f08f6b0fbb4711dc40b.png

Merging shapefiles with data#

clim = pd.read_csv('data/ma_clim.csv')
clim.head()
id life_expectancy self_reported_physical_health self_reported_mental_health drug_overdose_deaths_per_100_000_people alcohol_abuse suicide_rates current_diabetes current_adult_asthma stroke ... social_economic infrastructure environment cc_health cc_social_economic cc_extreme_events baseline climate_change cvi_overall geo_id
0 34984 0.463466 0.546088 0.629462 0.603549 0.373029 0.365998 0.394437 0.486654 0.275036 ... 0.538874 0.244333 0.797744 0.343846 0.419473 0.912341 0.496797 0.601826 0.547525 25017311700
1 34985 0.842463 0.752245 0.806395 0.603549 0.175318 0.365998 0.636471 0.650460 0.394204 ... 0.603291 0.413532 0.782838 0.327543 0.404224 0.912341 0.633500 0.583265 0.654402 25017311800
2 34986 0.886306 0.987106 0.972870 0.603549 0.238639 0.365998 0.913464 0.954555 0.930724 ... 0.873837 0.541954 0.796813 0.260636 0.412724 0.912341 0.858999 0.525501 0.830267 25017311900
3 34988 0.594612 0.821014 0.903088 0.603549 0.487845 0.365998 0.546841 0.871304 0.584045 ... 0.798237 0.470735 0.697917 0.390933 0.444987 0.976046 0.692181 0.768630 0.786493 25017312100
4 34993 0.188828 0.252710 0.270477 0.603549 0.798826 0.365998 0.125561 0.516453 0.275036 ... 0.316648 0.195124 0.614488 0.305656 0.315402 0.976169 0.241294 0.659768 0.354167 25017312502

5 rows × 233 columns

clim.columns = list(clim.columns)[:-1]+['GEOID']
clim.head()
id life_expectancy self_reported_physical_health self_reported_mental_health drug_overdose_deaths_per_100_000_people alcohol_abuse suicide_rates current_diabetes current_adult_asthma stroke ... social_economic infrastructure environment cc_health cc_social_economic cc_extreme_events baseline climate_change cvi_overall GEOID
0 34984 0.463466 0.546088 0.629462 0.603549 0.373029 0.365998 0.394437 0.486654 0.275036 ... 0.538874 0.244333 0.797744 0.343846 0.419473 0.912341 0.496797 0.601826 0.547525 25017311700
1 34985 0.842463 0.752245 0.806395 0.603549 0.175318 0.365998 0.636471 0.650460 0.394204 ... 0.603291 0.413532 0.782838 0.327543 0.404224 0.912341 0.633500 0.583265 0.654402 25017311800
2 34986 0.886306 0.987106 0.972870 0.603549 0.238639 0.365998 0.913464 0.954555 0.930724 ... 0.873837 0.541954 0.796813 0.260636 0.412724 0.912341 0.858999 0.525501 0.830267 25017311900
3 34988 0.594612 0.821014 0.903088 0.603549 0.487845 0.365998 0.546841 0.871304 0.584045 ... 0.798237 0.470735 0.697917 0.390933 0.444987 0.976046 0.692181 0.768630 0.786493 25017312100
4 34993 0.188828 0.252710 0.270477 0.603549 0.798826 0.365998 0.125561 0.516453 0.275036 ... 0.316648 0.195124 0.614488 0.305656 0.315402 0.976169 0.241294 0.659768 0.354167 25017312502

5 rows × 233 columns

clim['GEOID'].head()

0    25017311700
1    25017311800
2    25017311900
3    25017312100
4    25017312502
Name: GEOID, dtype: int64

clim['GEOID'] = clim['GEOID'].astype(str)
ma['GEOID'] = ma['GEOID'].astype(str)

list(clim.columns)[-10:]

['social_economic',
 'infrastructure',
 'environment',
 'cc_health',
 'cc_social_economic',
 'cc_extreme_events',
 'baseline',
 'climate_change',
 'cvi_overall',
 'GEOID']

data_col = 'cvi_overall'

ma_new = ma.merge(clim[['GEOID',data_col]], how='left', on='GEOID')
ma_new.head()
STATEFP COUNTYFP TRACTCE GEOID NAME NAMELSAD MTFCC FUNCSTAT ALAND AWATER INTPTLAT INTPTLON geometry cvi_overall
0 25 009 265102 25009265102 2651.02 Census Tract 2651.02 G5020 S 16318373 134252 +42.7338220 -070.9600766 POLYGON ((-70.99091 42.73399, -70.99089 42.734... 0.259322
1 25 009 268200 25009268200 2682 Census Tract 2682 G5020 S 10737361 364499 +42.8117773 -070.9054643 POLYGON ((-70.92052 42.79103, -70.9205 42.7910... 0.513305
2 25 009 268400 25009268400 2684 Census Tract 2684 G5020 S 3065747 4715475 +42.8054407 -070.8329685 POLYGON ((-70.87547 42.79793, -70.87547 42.797... 0.238324
3 25 009 250500 25009250500 2505 Census Tract 2505 G5020 S 300558 3894 +42.7169313 -071.1693673 POLYGON ((-71.17166 42.72127, -71.1709 42.7208... 0.798346
4 25 027 731300 25027731300 7313 Census Tract 7313 G5020 S 743090 7345 +42.2513743 -071.8152408 POLYGON ((-71.82361 42.24948, -71.8228 42.2499... 0.530552 
from matplotlib.patches import Patch
from matplotlib import colormaps
import matplotlib.cm as cm

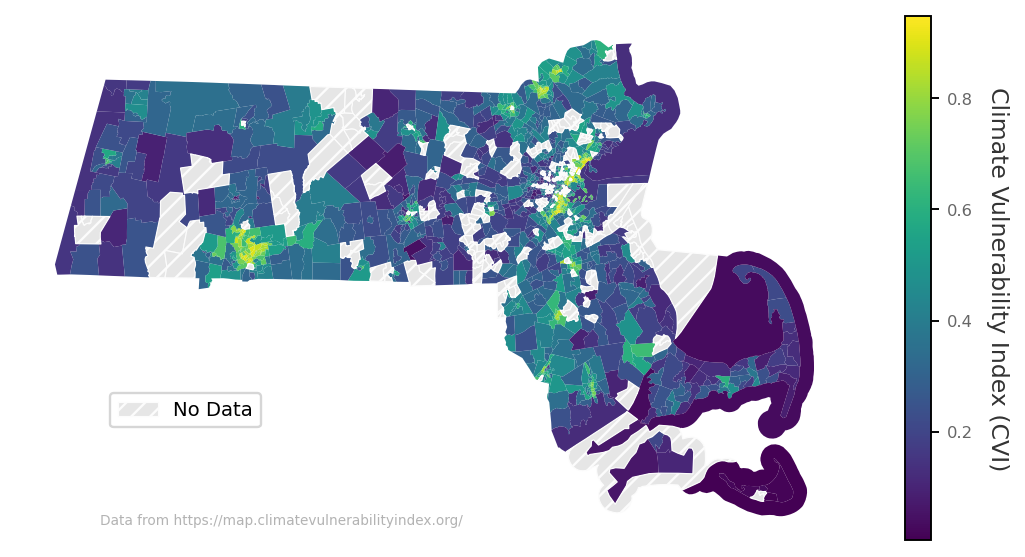
fig, ax = plt.subplots(1, 1, figsize=(8, 4), dpi=170)

cmap = colormaps['viridis']
norm = plt.Normalize(vmin=ma_new[data_col].min(), vmax=ma_new[data_col].max())

# Plot the data with the colormap for non-missing values
ma_new[ma_new[data_col].notna()].plot(column=data_col, cmap=cmap, ax=ax)

# Add the missing data with a checkered (hatched) pattern
ma_new[ma_new[data_col].isna()].plot(ax=ax, color='.9', edgecolor='.99', lw=0.5, hatch='///')

# Create a custom legend
ax.legend(handles=[Patch(facecolor='.9', edgecolor='.99', hatch='///',
                         lw=0.5, label='No Data')],
          loc=2, bbox_to_anchor=[0.1,0.3], fontsize='small')

# Add a colorbar with a label
sm = cm.ScalarMappable(cmap=cmap, norm=norm)  # ScalarMappable for the colorbar
sm._A = []  # Dummy array for ScalarMappable
cbar = fig.colorbar(sm, ax=ax, orientation='vertical')  # Add colorbar to the plot
cbar.set_label('Climate Vulnerability Index (CVI)', rotation=270, labelpad=15, color='.2')
cbar.ax.tick_params(labelsize='x-small', labelcolor='.4')

ax.text(0.1, 0.025, 'Data from https://map.climatevulnerabilityindex.org/', color='.7', fontsize='xx-small',
        ha='left', va='bottom', transform=ax.transAxes)
ax.set_axis_off()


plt.show()
_images/71d30bc5a3f37ebf733d33e5278983584cfd523a72640817b5a8cd3474cdd14d.png

Tons more great resources here:#

mszell/geospatialdatascience

Spatial Joins in Geopandas#

Spatial joins are a powerful GIS operation that combines attributes from two datasets based on their spatial relationships. Unlike traditional tabular joins, which rely on matching keys, spatial joins depend on how geometries interact, such as whether one geometry contains another or overlaps with it. For example, you can use spatial joins to determine which census tract a point (like a school or store) falls into or to aggregate data by spatial boundaries. See terrific tutorial about spatial joins here: https://pygis.io/docs/e_spatial_joins.html! Drawing a bunch from it’s great materials below.

We’ll practice by performing spatial joins to associate point data with Massachusetts (MA) census tracts. We’ll generate random points within the bounding box of the MA shapefile and join these points to their corresponding census tracts.

Exercise: We’re going to randomly generate points data throughout the bounding box of MA, and spatial join these points to census tracts.

minx, miny, maxx, maxy = ma.total_bounds
print(f"Bounding box: ({minx}, {miny}, {maxx}, {maxy})")

n_points = 10000

# Generate random latitudes and longitudes within the bounding box
random_lons = np.random.uniform(minx, maxx, n_points)
random_lats = np.random.uniform(miny, maxy, n_points)

random_points = pd.DataFrame({'lat':random_lats,'lon':random_lons})

Bounding box: (-73.50820999999999, 41.187053, -69.85886099999999, 42.886778)

random_points.head()
lat lon
0 41.348976 -72.716133
1 42.653198 -70.076800
2 42.702141 -71.039571
3 42.487032 -71.647537
4 42.075592 -70.850412 
fig, ax = plt.subplots(1,2,figsize=(20,5.65),dpi=100,
                       gridspec_kw={'width_ratios':[1,1]},sharex=True,sharey=True)

ax[0].scatter(random_points['lon'].values,random_points['lat'].values,color='.2', s=2, lw=0)

ma.plot(ax=ax[1])

plt.show()
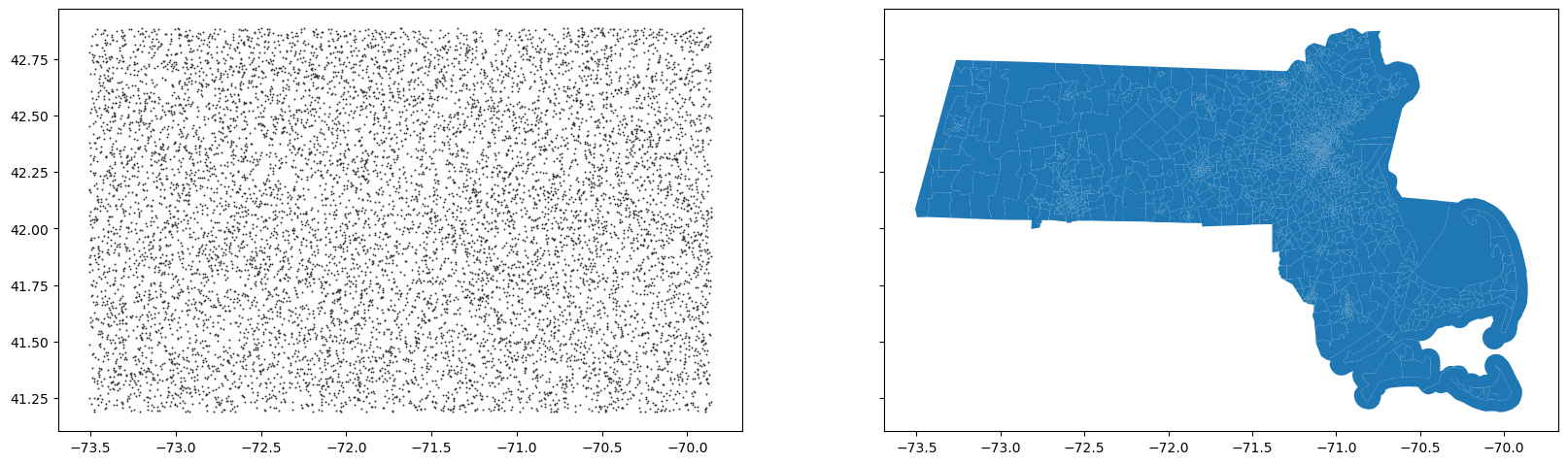
_images/5ab0f3d53d8a84e01f3a3bc1906aa4dad269e65116a737eed118ae90e7fa8e81.png

We’ll need a GeoDataFrame in order to do the spatial join!

from shapely.geometry import Point
# Create a GeoDataFrame for these points
random_points = gpd.GeoDataFrame({
    'id': range(n_points),  # Assign unique IDs
    'latitude': random_lats,
    'longitude': random_lons
}, geometry=[Point(xy) for xy in zip(random_lons, random_lats)], crs="EPSG:4326")

fig, ax = plt.subplots(figsize=(10, 10))

# Plot census tracts
ma.plot(ax=ax, fc='lightblue',ec='.4', linewidth=0.5)
# ma.boundary.plot(ax=ax, color='black', linewidth=0.5)

# Plot random points
random_points.plot(ax=ax, color='red', markersize=1, label='Random Points')

# Add legend and title
plt.legend(framealpha=1, loc=3)
plt.title('Random Points within MA Census Tracts')
plt.show()
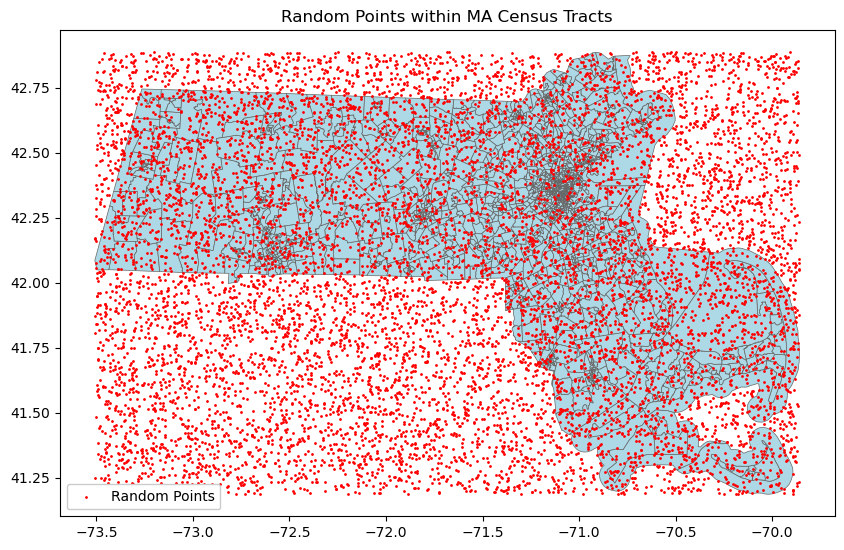
_images/f4515ed012585093180dfedd2f6094550bb022abc8ab975d3b985f2ab461c982.png 
points_with_tracts = gpd.sjoin(random_points, ma, how='left', predicate='within')

/tmp/ipykernel_4309/2835737534.py:1: UserWarning: CRS mismatch between the CRS of left geometries and the CRS of right geometries.
Use `to_crs()` to reproject one of the input geometries to match the CRS of the other.

Left CRS: EPSG:4326
Right CRS: EPSG:4269

  points_with_tracts = gpd.sjoin(random_points, ma, how='left', predicate='within')

Oh no! CRS :(

print(random_points.crs)  # Should be EPSG:4326
print(ma.crs)  # Should be EPSG:4269

EPSG:4326
EPSG:4269

random_points = random_points.to_crs(ma.crs)

points_with_tracts = gpd.sjoin(random_points, ma, how='left', predicate='within')

# Count points in each census tract
points_per_tract = points_with_tracts.groupby('GEOID').size().reset_index(name='point_count')

# Merge counts back to census tracts
ma_tracts_with_counts = ma.merge(points_per_tract, on='GEOID', how='left')
ma_tracts_with_counts['point_count'] = ma_tracts_with_counts['point_count'].fillna(0)

ma_tracts_with_counts
STATEFP COUNTYFP TRACTCE GEOID NAME NAMELSAD MTFCC FUNCSTAT ALAND AWATER INTPTLAT INTPTLON geometry point_count
0 25 009 265102 25009265102 2651.02 Census Tract 2651.02 G5020 S 16318373 134252 +42.7338220 -070.9600766 POLYGON ((-70.99091 42.73399, -70.99089 42.734... 1.0
1 25 009 268200 25009268200 2682 Census Tract 2682 G5020 S 10737361 364499 +42.8117773 -070.9054643 POLYGON ((-70.92052 42.79103, -70.9205 42.7910... 3.0
2 25 009 268400 25009268400 2684 Census Tract 2684 G5020 S 3065747 4715475 +42.8054407 -070.8329685 POLYGON ((-70.87547 42.79793, -70.87547 42.797... 0.0
3 25 009 250500 25009250500 2505 Census Tract 2505 G5020 S 300558 3894 +42.7169313 -071.1693673 POLYGON ((-71.17166 42.72127, -71.1709 42.7208... 0.0
4 25 027 731300 25027731300 7313 Census Tract 7313 G5020 S 743090 7345 +42.2513743 -071.8152408 POLYGON ((-71.82361 42.24948, -71.8228 42.2499... 0.0
... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
1615 25 025 070802 25025070802 708.02 Census Tract 708.02 G5020 S 129953 0 +42.3417055 -071.0802334 POLYGON ((-71.08315 42.34162, -71.08303 42.341... 0.0
1616 25 025 061202 25025061202 612.02 Census Tract 612.02 G5020 S 380810 4897 +42.3387527 -071.0625085 POLYGON ((-71.06553 42.33603, -71.06551 42.336... 1.0
1617 25 025 070801 25025070801 708.01 Census Tract 708.01 G5020 S 61235 0 +42.3399771 -071.0825322 POLYGON ((-71.08468 42.34029, -71.08431 42.340... 0.0
1618 25 025 060601 25025060601 606.01 Census Tract 606.01 G5020 S 140332 0 +42.3392514 -071.0489604 POLYGON ((-71.05238 42.3398, -71.0519 42.34019... 0.0
1619 25 025 070901 25025070901 709.01 Census Tract 709.01 G5020 S 57691 0 +42.3377169 -071.0795662 POLYGON ((-71.08181 42.33856, -71.08116 42.338... 0.0

1620 rows × 14 columns

fig, ax = plt.subplots(1,1,figsize=(10, 5), dpi=200)

# Plot census tracts colored by the number of points
ma_tracts_with_counts.plot(column='point_count', lw=0.25, 
                           ec='.2', cmap='OrRd', legend=True, ax=ax)

# Plot random points
random_points.plot(ax=ax, color='blue', markersize=1, lw=0, label='Random Points', alpha=0.2)

# Add legend and title
ax.legend(loc=3)
ax.set_title('Points Per Census Tract')

plt.show()
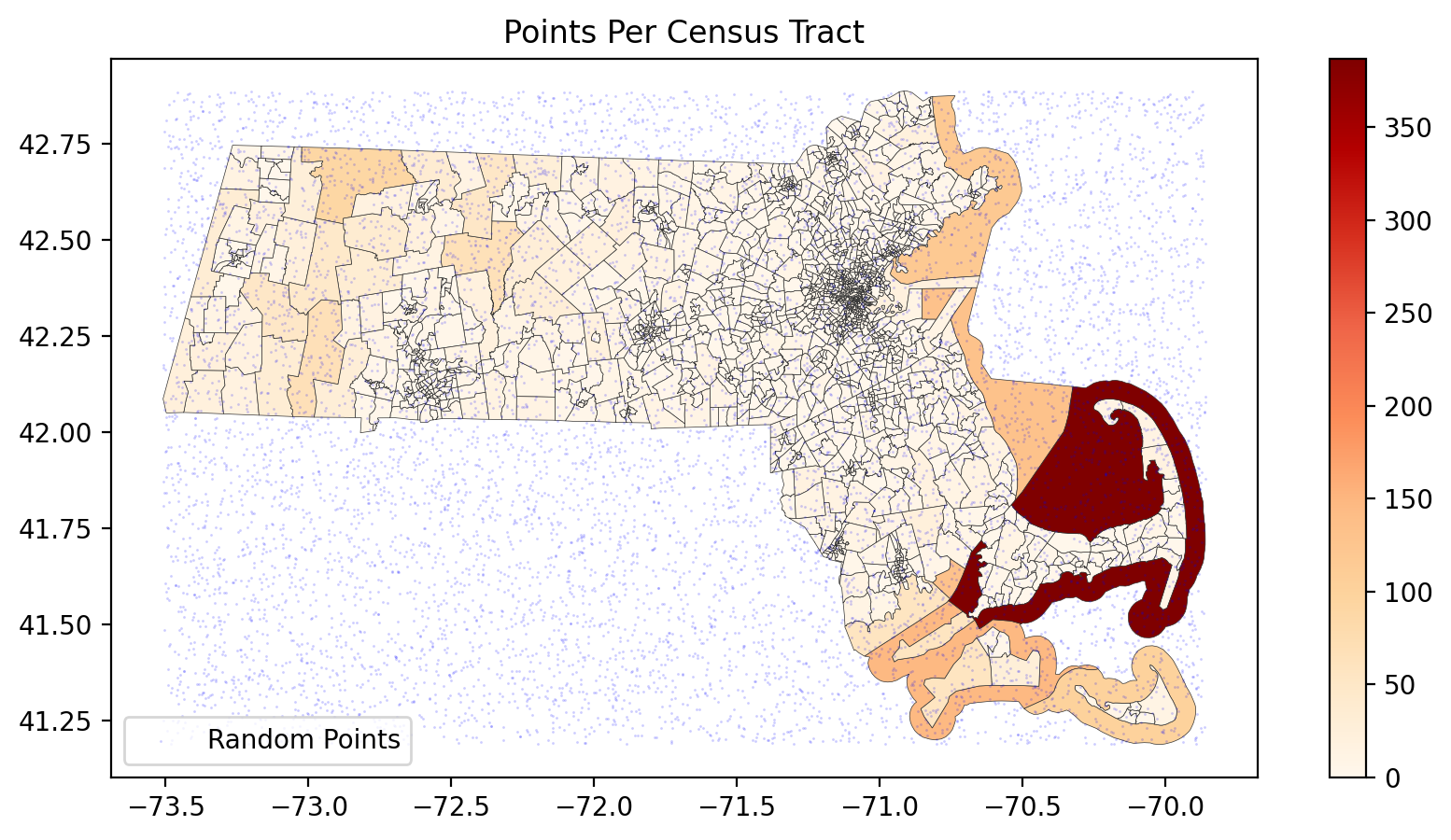
_images/a1a60740dce4888c3f8702f410d099edd913bdb26d7e99d2a571b096415d920d.png

If there’s time…#

Try to find point data that you can spatially join with shapefile data. What challenges might you foresee?

pass

Next time…#

There is no next time!!

References and further resources:#

  1. Class Webpages

  2. Penrose, M. D. (2003). Random Geometric Graphs. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780198506263.001.0001

  3. Gilbert, E. N. (1961). Random plane networks. Journal of the Society for Industrial and Applied Mathematics, 9(4), 533–543. https://doi.org/10.1137/0109045

  4. Dall, J., & Christensen, M. (2002). Random geometric graphs. Physical Review E, 66(1), 016121. https://doi.org/10.1103/PhysRevE.66.016121

  5. Penrose, M. D. (1999). On \(k\)-connectivity for a geometric random graph. Random Structures & Algorithms, 15(2), 145–164. https://doi.org/10.1002/(SICI)1098-2418(199909)15:2<145::AID-RSA2>3.0.CO;2-G

  6. Barthelemy, M. (2011). Spatial networks. Physics Reports, 499(1–3), 1–101. https://doi.org/10.1016/j.physrep.2010.11.002

  7. Haenggi, M. (2009). Stochastic Geometry for Wireless Networks. Cambridge University Press. https://doi.org/10.1017/CBO9781139043816

  8. Eppstein, D., Goodrich, M. T., & Trott, L. (2009, November). Going off-road: transversal complexity in road networks. In Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems (pp. 23-32). https://doi.org/10.1145/1653771.1653778

  9. Boeing, G. (2024). Modeling and Analyzing Urban Networks and Amenities with OSMnx. Working paper. https://geoffboeing.com/publications/osmnx-paper/.

  10. Boeing, G. (2017). OSMnx: New methods for acquiring, constructing, analyzing, and visualizing complex street networks. Computers, Environment and Urban Systems, 65, 126–139. https://doi.org/10.1016/j.compenvurbsys.2017.05.004.

  11. Boeing, G. (2022). Street network models and indicators for every urban area in the world. Geographical Analysis, 54(3), 519-535. https://doi.org/10.1111/gean.12281.